DerivKit documentation¶

Contents:

DerivKit is a robust Python toolkit for stable numerical derivatives, built for scientific computing, cosmology, and any domain requiring accurate gradients or higher-order expansions.

It provides:

Adaptive polynomial fitting that excludes noisy points based on residuals,
High-order finite differences for accurate stencil-based derivatives,
A simple API for comparing both approaches side by side.

Detailed documentation of the toolkit’s modules can be found in the sidebar.

Installation¶

pip install derivkit

Quick Start¶

from derivkit import DerivativeKit

def simple_function(x):
    return x**2 + x

dk = DerivativeKit(
  function=simple_function,
  x0=1.0
)
print("Adaptive:", dk.differentiate(order=1, method="adaptive"))
print("Finite Difference:", dk.differentiate(order=1, method="finite"))

Method Overview¶

The following table summarizes the current and planned derivative engines in DerivKit:

Method	Status	Uses / Philosophy	Notes
Finite Difference	Implemented	Local differences — Estimate slope from nearby points.	High-order stencils, stable up to 9-point central schemes.
Adaptive Fit	Implemented	Local polynomial regression — Fit a small local model and read off derivative.	Robust against noise; uses residual-based trimming.
Gaussian Process	In Progress	Probabilistic interpolation — Fit a stochastic model, then differentiate the posterior mean.	Uses RBF kernel; fits mean and variance jointly.
Fornberg (analytic)	In Progress	Analytic finite-difference weights from the Fornberg algorithm.	Exact stencil construction; used for validation suite.
Complex Step	Planned	Perturb in the complex plane to avoid subtraction error.	For analytic smooth functions only.

Adaptive Fit Example¶

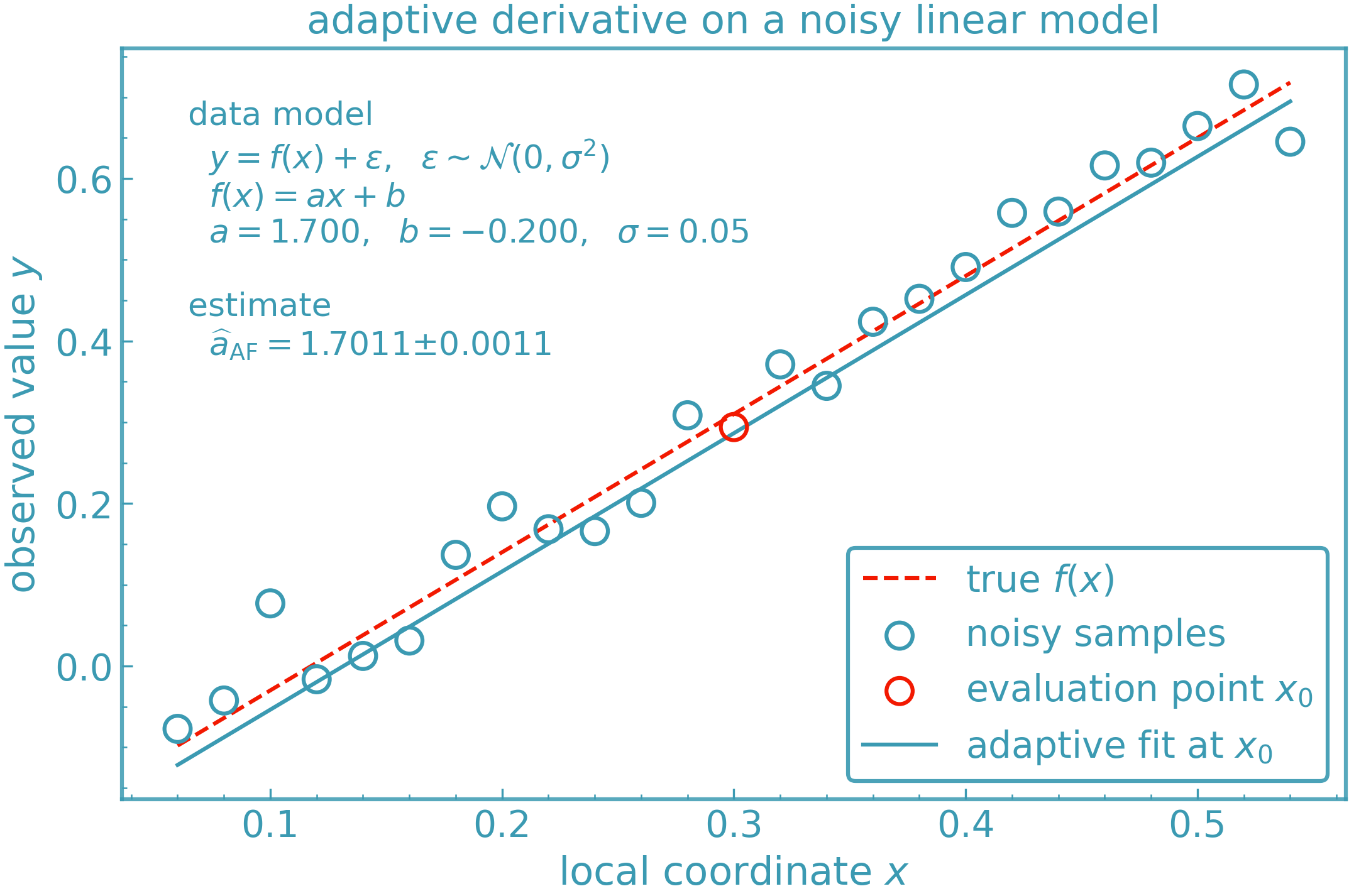
Below is a visual example of the derivkit.adaptive_fit module estimating the first derivative of a nonlinear function in the presence of noise. The method selectively discards outlier points before fitting a polynomial, resulting in a robust and smooth estimate.

_images/adaptive_demo_linear_noisy_order1.png

Citation¶

If you use derivkit in your research, please cite it as follows:

@software{sarcevic2025derivkit,
  author       = {Nikolina Šarčević and Matthijs van der Wild and Cynthia Trendafilova and Bastien Carreres},
  title        = {derivkit: A Python Toolkit for Numerical Derivatives},
  year         = {2025},
  publisher    = {GitHub},
  journal      = {GitHub Repository},
  howpublished = {\url{https://github.com/derivkit/derivkit}},
}

Contributing¶

Interested in getting involved? Have a look at Contributing!