DerivKit logo black DerivativeKit#

DerivKit implements several complementary derivative engines. Each has different strengths depending on smoothness, noise level, and computational cost.

This page gives an overview of the main methods featured in DerivativeKit, how they work, and when to use each one.

All methods are accessed through the same DerivativeKit interface and can be swapped without changing downstream code.

Runnable examples illustrating these methods are collected in Examples.

Finite Differences#

How it works:

Estimate derivatives by evaluating the function at points around x0 and combining them into a central-difference stencil [1].

In general, a central finite-difference approximation to the first derivative can be written as a weighted sum over function evaluations at symmetric offsets around x0:

\[f'(x_0) \approx \frac{1}{h} \sum_{k=-m}^{m} c_k\, f(x_0 + k h),\]

where h is the step size (the spacing between adjacent stencil points), and the stencil coefficients c_k satisfy symmetry conditions (c_{-k} = -c_k) and are chosen to cancel low-order truncation errors. The integer m determines the stencil width (e.g. m=1 for a 3-point stencil, m=2 for a 5-point stencil). The coefficients c_k are computed using standard algorithms (such as Fornberg’s method), which construct finite-difference weights by enforcing the desired order of accuracy for a given stencil.

Higher-order stencils improve accuracy by cancelling additional error terms, at the cost of more function evaluations.

DerivKit implementation:

  • 3, 5, 7, 9-point central stencils

  • Richardson extrapolation [4] (reduces truncation error)

  • Ridders extrapolation [5] (adaptive error control)

  • Gauss–Richardson extrapolation (GRE) [3] (noise-robust variant)

Use when:

  • The function is smooth and cheap to evaluate

  • Noise is low or absent

  • You want fast derivatives with minimal overhead

Avoid when:

  • The function is noisy or discontinuous

  • Step-size tuning is difficult or unstable

  • Function evaluations are expensive

Examples:

A basic finite-difference example is shown in Finite differences.

Simple Polynomial Fit#

How it works:

Sample points in a small, user-controlled window around x0 and fit a fixed-order polynomial (e.g. quadratic or cubic) on a simple grid. The derivative at x0 is taken from the analytic derivative of the fitted polynomial [2].

The expression for a first derivative from a centered quadratic fit

\[p(x) = a_0 + a_1 (x - x_0) + a_2 (x - x_0)^2\]

is:

\[p'(x_0) = a_1,\]

where a_1 is the fitted linear coefficient of the polynomial.

DerivKit implementation:

  • User-chosen window and polynomial degree

  • Low overhead and easy to reason about

  • Includes diagnostics on fit quality and conditioning

Use when:

  • The function is smooth but mildly noisy

  • You want a simple, local smoothing method

  • A fixed window and polynomial degree are sufficient

Avoid when:

  • Noise is strong or highly irregular

  • The fit becomes ill-conditioned in the chosen window

Examples:

A basic polyfit example is shown in Local polynomial fit.

Adaptive Polynomial Fit#

How it works:

Build a Chebyshev-spaced grid around x0, rescale offsets to a stable interval, and fit a local polynomial with optional ridge regularisation. The method can enlarge the grid if there are too few samples, adjust the effective polynomial degree, and reports detailed diagnostics [2].

For a centered polynomial fit of degree d,

\[p(x) = \sum_{k=0}^{d} a_k (x - x_0)^k,\]

the first derivative is

\[p'(x) = \sum_{k=1}^{d} k\, a_k (x - x_0)^{k-1},\]

and in particular

\[p'(x_0) = a_1,\]

where a_k are the fitted polynomial coefficients.

Sampling strategy:

  • Default: symmetric Chebyshev nodes around x0 with automatic half-width (via spacing="auto" and base_abs)

  • Domain-aware: interval is clipped to stay inside a given (lo, hi) domain

  • Custom grids: user can supply explicit offsets or absolute sample locations

Below is a visual example of the derivkit.adaptive_fit module estimating the first derivative of a nonlinear function in the presence of noise. The method selectively discards outlier points before fitting a polynomial, resulting in a robust and smooth estimate.

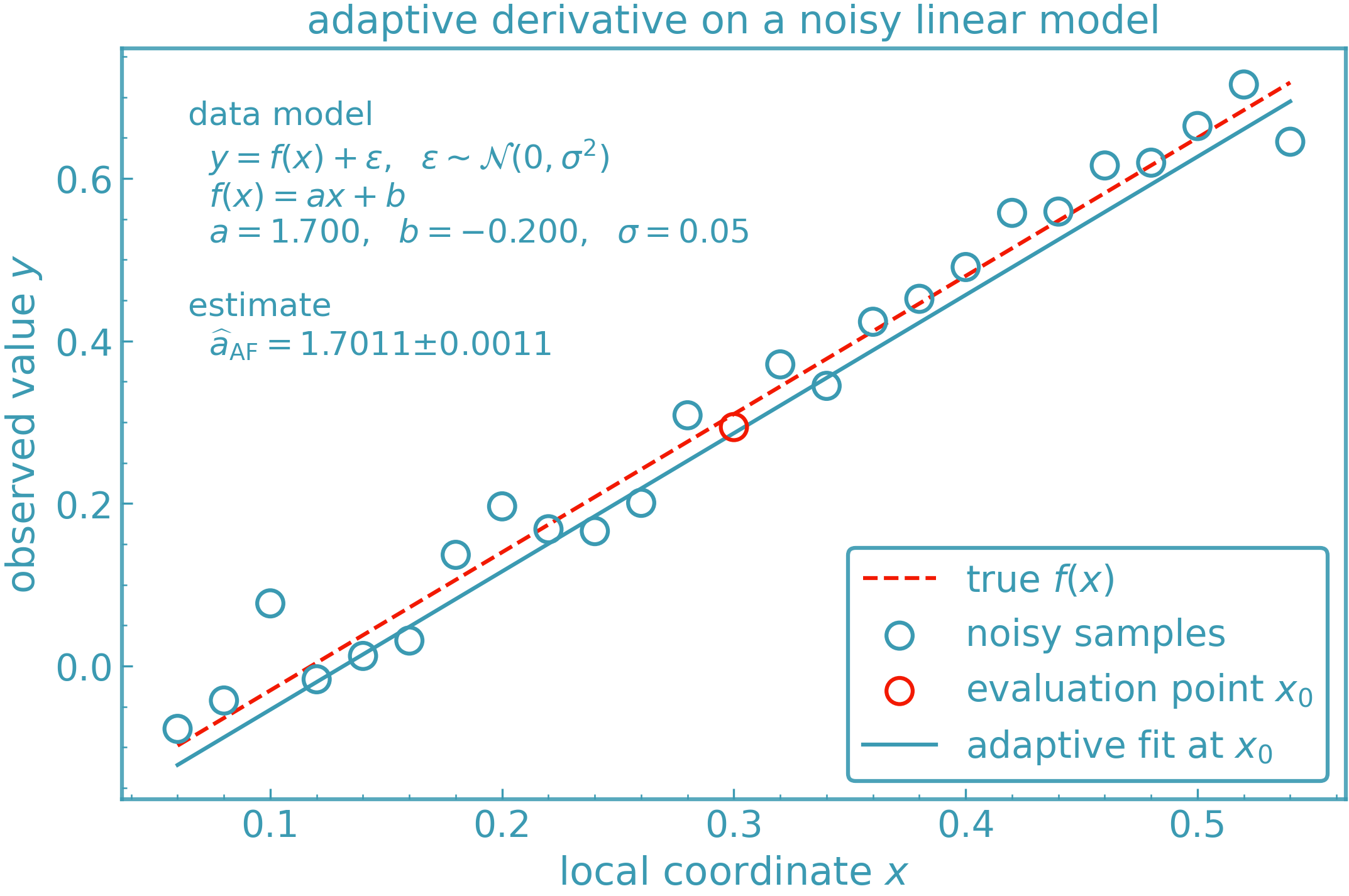
../../_images/adaptive_demo_linear_noisy_order1.png

DerivKit implementation:

  • Scales offsets before fitting to reduce conditioning

  • Optional ridge term to stabilise ill-conditioned Vandermonde systems

  • Checks fit quality and flags “obviously bad” derivatives with suggestions for improvement

  • Optional diagnostics dictionary with sampled points, fit metrics, and metadata

Use when:

  • The function is noisy, irregular, or numerically delicate

  • Finite differences or simple polyfits fail

  • You want diagnostics to understand derivative quality

Avoid when:

  • The function is extremely smooth and cheap to evaluate

  • Minimal overhead is a priority

  • You want a minimal-overhead solution for very smooth functions

Examples:

A basic adaptive polyfit example is shown in Adaptive polynomial fit.

Tabulated Functions#

How it works:

When the target function is provided as tabulated data (x, y), DerivKit first wraps the table in a lightweight interpolator and then applies any of the available derivative engines to the interpolated function.

Internally, tabulated data are represented by derivkit.tabulated_model.one_d.Tabulated1DModel, which exposes a callable interface compatible with all derivative methods.

DerivKit implementation:

  • Supports scalar-, vector-, and tensor-valued tabulated outputs

  • Uses fast linear interpolation via numpy.interp

  • Seamlessly integrates with finite differences, adaptive fit, local polynomial, and Fornberg methods

  • Identical API to function-based differentiation via DerivativeKit

Use when:

  • The function is only available as discrete samples

  • Evaluating the function on demand is expensive or impossible

  • You want to reuse DerivKit’s derivative engines on interpolated data

Avoid when:

  • The tabulation is too coarse to resolve derivatives

  • The function has sharp features not captured by interpolation

  • Exact derivatives are required

Examples:

See Tabulated derivatives for a basic example using tabulated data.

JAX Autodiff#

How it works:

JAX provides automatic differentiation for Python functions written using jax.numpy <https://docs.jax.dev/en/latest/jax.numpy.html>. Instead of estimating derivatives numerically, autodiff propagates derivatives analytically through the computational graph, yielding exact derivatives up to machine precision.

This avoids step-size choices, local sampling, and numerical differencing. However, this does not imply that autodiff is universally superior. A common misconception is that autodiff always yields a “perfect” derivative: in practice, it differentiates the implemented computation, which may already include approximations, interpolation, or numerical artifacts. As a result, autodiff can produce an exact derivative of an effective function that differs from the intended underlying model.

Its applicability is therefore limited to fully JAX-compatible, analytic models and does not extend to noisy, interpolated, or externally evaluated functions.

DerivKit implementation:

  • Exposed as an optional reference backend and not registered as a standard DerivativeKit method

  • Intended primarily for sanity checks and validation

  • Not a core focus of DerivKit, which targets workflows where models are:

    • noisy

    • tabulated

    • interpolated

    • externally evaluated

    • incompatible with automatic differentiation

Use when:

  • The function is analytic and fully JAX-compatible

  • You want an exact reference derivative for comparison

  • You are prototyping or testing derivative workflows

Avoid when:

  • The function is noisy, tabulated, interpolated, or provided by an external numerical code (e.g. Boltzmann solvers or emulators in cosmology)

  • You need production robustness or broad applicability

  • JAX compatibility cannot be guaranteed

In most scientific workflows targeted by DerivKit, the adaptive polynomial fit or finite-difference methods above are more appropriate.

Installation details for the JAX module are described in Installation. We do not recommend JAX for production use within DerivKit at this time.

References#