Fisher bias#

This section shows how to map a systematic-induced shift in the data vector into a parameter shift using derivkit.forecast_kit.ForecastKit.

The Fisher-bias workflow takes:

a Fisher matrix F (typically from derivkit.forecast_kit.ForecastKit.fisher())
a difference data vector delta_nu (systematic shift in observables)

and returns:

the Fisher-bias vector in parameter space \(b_a\)
the corresponding first-order parameter shift \(\Delta \theta_a\).

For a conceptual overview of Fisher bias, its interpretation, and other forecasting frameworks in DerivKit see ForecastKit.

Compute `delta_nu`#

derivkit.forecast_kit.ForecastKit.delta_nu() computes a consistent 1D difference vector. It accepts 1D arrays or 2D arrays (which are flattened in row-major (“C”) order to match the package convention).

>>> import numpy as np
>>> from derivkit.forecast_kit import ForecastKit
>>> np.set_printoptions(precision=8, suppress=True)
>>> # Define a simple toy model
>>> def model(theta0):
...     theta1, theta2 = theta0
...     return np.array([theta1, theta2, theta1 + 2.0 * theta2], dtype=float)
>>> # Fiducial parameters and covariance
>>> theta0 = np.array([1.0, 2.0])
>>> cov = np.eye(3)
>>> fk = ForecastKit(function=model, theta0=theta0, cov=cov)
>>> # Construct unbiased and biased data vectors
>>> data_unbiased = model(theta0)
>>> data_biased = data_unbiased + np.array([0.5, -0.8, 0.3])
>>> # Compute difference data vector Δν
>>> dn = fk.delta_nu(data_unbiased=data_unbiased, data_biased=data_biased)
>>> print(dn)
[ 0.5  -0.8   0.3]
>>> print(dn.shape)
(3,)

Compute Fisher bias and parameter shifts#

Use derivkit.forecast_kit.ForecastKit.fisher_bias() to compute the bias vector and the corresponding parameter shift.

>>> import numpy as np
>>> from derivkit.forecast_kit import ForecastKit
>>> np.set_printoptions(precision=8, suppress=True)
>>> # Define a simple toy model
>>> def model(theta0):
...     theta1, theta2 = theta0
...     return np.array([theta1, theta2, theta1 + 2.0 * theta2], dtype=float)
>>> # Fiducial setup
>>> theta0 = np.array([1.0, 2.0])
>>> cov = np.eye(3)
>>> fk = ForecastKit(function=model, theta0=theta0, cov=cov)
>>> # Compute Fisher matrix
>>> fisher = fk.fisher()
>>> # Build systematic difference vector
>>> data_unbiased = model(theta0)
>>> data_biased = data_unbiased + np.array([0.5, -0.8, 0.3])
>>> dn = fk.delta_nu(data_unbiased=data_unbiased, data_biased=data_biased)
>>> # Compute Fisher bias and parameter shift
>>> bias_vec, delta_theta = fk.fisher_bias(fisher_matrix=fisher, delta_nu=dn)
>>> print(bias_vec)
[ 0.8 -0.2]
>>> print(delta_theta)
[ 0.73333333 -0.33333333]

Using a specific derivative backend#

You can pass method and backend-specific options (forwarded to derivkit.derivative_kit.DerivativeKit.differentiate()) for consistent derivative control across Fisher and Fisher-bias calculations.

>>> import numpy as np
>>> from derivkit.forecast_kit import ForecastKit
>>> np.set_printoptions(precision=8, suppress=True)
>>> # Define a simple toy model
>>> def model(theta0):
...     theta1, theta2 = theta0
...     return np.array([theta1, theta2, theta1 + 2.0 * theta2], dtype=float)
>>> theta0 = np.array([1.0, 2.0])
>>> cov = np.eye(3)
>>> fk = ForecastKit(function=model, theta0=theta0, cov=cov)
>>> # Compute Fisher matrix with finite-difference backend
>>> fisher = fk.fisher(method="finite", stepsize=1e-2, num_points=5, extrapolation="ridders", levels=4)
>>> # Construct difference data vector
>>> dn = fk.delta_nu(
...     data_unbiased=model(theta0),
...     data_biased=model(theta0) + np.array([0.5, -0.8, 0.3]),
... )
>>> # Compute Fisher bias using the same backend
>>> bias_vec, delta_theta = fk.fisher_bias(
...     fisher_matrix=fisher,
...     delta_nu=dn,
...     method="finite",
...     stepsize=1e-2,
...     num_points=5,
...     extrapolation="ridders",
...     levels=4,
... )
>>> print(bias_vec)
[ 0.8 -0.2]
>>> print(delta_theta)
[ 0.73333333 -0.33333333]

Fisher bias contours with GetDist#

You can visualize the impact of a systematic as a shift of the Fisher forecast contours: plot the original Fisher Gaussian at theta0 and the biased one at theta0 + delta_theta (same covariance, shifted mean).

>>> import numpy as np
>>> from getdist import plots as getdist_plots
>>> from derivkit.forecast_kit import ForecastKit
>>> from derivkit.forecasting.getdist_fisher_samples import fisher_to_getdist_gaussiannd
>>> # Define a simple toy model
>>> def model(theta0):
...     theta1, theta2 = theta0
...     return np.array([theta1, theta2, theta1 + 2.0 * theta2], dtype=float)
>>> # Fiducial parameters and covariance
>>> theta0 = np.array([1.0, 2.0])
>>> cov = np.eye(3)
>>> # Build ForecastKit and compute Fisher matrix
>>> fk = ForecastKit(function=model, theta0=theta0, cov=cov)
>>> fisher = fk.fisher(method="finite", stepsize=1e-2, num_points=5, extrapolation="ridders", levels=4)
>>> # Construct difference data vector
>>> data_unbiased = model(theta0)
>>> data_biased = data_unbiased + np.array([0.5, -0.8, 0.3])
>>> dn = fk.delta_nu(data_unbiased=data_unbiased, data_biased=data_biased)
>>> bias_vec, delta_theta = fk.fisher_bias(fisher_matrix=fisher, delta_nu=dn)
>>> # Convert Fisher matrices to GetDist Gaussians
>>> gnd_unbiased = fisher_to_getdist_gaussiannd(
...     theta0=theta0,
...     fisher=fisher,
...     names=["theta1", "theta2"],
...     labels=[r"\theta_1", r"\theta_2"],
...     label="Unbiased",
... )
>>> gnd_biased = fisher_to_getdist_gaussiannd(
...     theta0=theta0 + delta_theta,
...     fisher=fisher,
...     names=["theta1", "theta2"],
...     labels=[r"\theta_1", r"\theta_2"],
...     label="Biased",
... )
>>> # Plot biased and unbiased contours
>>> dk_red = "#f21901"
>>> dk_yellow = "#e1af00"
>>> line_width = 1.5
>>> plotter = getdist_plots.get_subplot_plotter(width_inch=3.6)
>>> plotter.settings.linewidth_contour = line_width
>>> plotter.settings.linewidth = line_width
>>> plotter.settings.figure_legend_frame = False
>>> plotter.triangle_plot(
...     [gnd_unbiased, gnd_biased],
...     params=["theta1", "theta2"],
...     legend_labels=["Unbiased", "Biased"],
...     legend_ncol=1,
...     filled=[False, False],
...     contour_colors=[dk_yellow, dk_red],
...     contour_lws=[line_width, line_width],
...     contour_ls=["-", "-"],
... )
>>> bool(np.all(np.isfinite(delta_theta)))
True

(png)

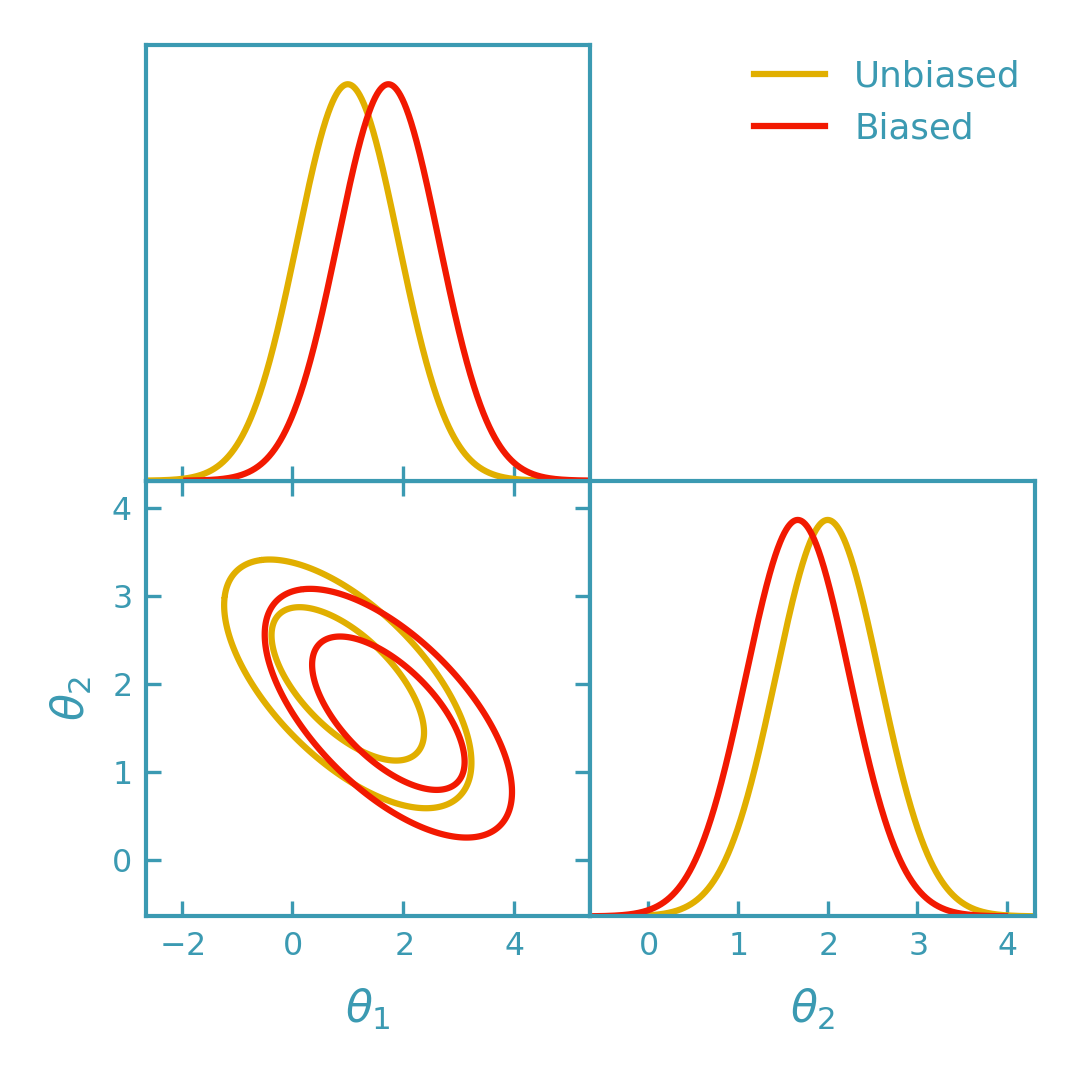
Notes#

delta_nu corresponds to the difference data vector \(\Delta \nu = \nu^{\mathrm{biased}} - \nu^{\mathrm{unbiased}}\), evaluated consistently with the covariance. Notice the convention and sign as the interpretaton of the results depend on it.
The Fisher bias approximation is local: derivatives are evaluated at theta0.
The returned delta_theta is the first-order parameter shift implied by the systematic difference vector.
All examples in this section use mock data and toy systematics for illustration only. The injected delta_nu and the resulting Fisher bias are arbitrary and chosen to produce a visible parameter shift. In a real analysis, delta_nu should be derived from a physically motivated systematic model evaluated consistently with the data vector and covariance.